Heat Transfer and the Human Body
1. Introduction
Humans, and animals in general, are usually in a thermal steady state with respect to their surroundings. In particular, endotherms seek to control their body temperatures. Heat generated by metabolic processes is lost to the environment though several mechanisms: radiation, conduction, convection, and evaporation. Unless the organism has more heat than can be eliminated by radiation and convection, evaporation (through perspiration) is not required and conduction is negligible (cf. section 2). This is most relevant when ambient temperatures are low (e.g., winter). While radiation is easily estimated, convection requires more effort and some assumptions.
2. Free convection
Convection relies on the flow of a fluid to transport heat from the object being cooled to the surrounding environment. In free convection, this fluid motion is the result of the buoyancy of warmer fluid in the cooler surrounding fluid. If there is an externally imposed flow, such as a wind, the convective rate is enhanced. At the very least, heat will be removed at the rate due to free convection. The Nusselt number is the ratio of the hard-to-compute convective transfer rate to the easy-to-determine conductive rate:1
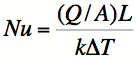 (1)
(1)
where Q/A is the
thermal flux (W/m2), L is the characteristic length of the body, k is the thermal
conductivity of the fluid, and ΔT is the temperature difference between the
body and the surrounding fluid. The Nusselt number can be found
by computing the Grashof number and the Prandtl number. Those
fluid dynamicists love all their special numbers, don't they?
The Grashof number is given by2
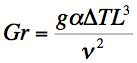 (2)
where α is the thermal expansion coefficient and the other
symbols have their usual meanings, defined in the reference. The
Prandtl number is simply the ratio of the kinematic viscosity to
the thermal diffusivity. For air, Pr is approximately 0.7, depending slightly on
temperature.3 The product, Gr*Pr is the Rayleigh number, Ra, which can be used to
find the Nusselt number. The relationship between Nu and Ra is empirical. For this,
we must turn to a heat transfer text.4 As we will
see, Ra is about 1010,
which puts us at the top of the transition region and into the
turbulent region, where
(2)
where α is the thermal expansion coefficient and the other
symbols have their usual meanings, defined in the reference. The
Prandtl number is simply the ratio of the kinematic viscosity to
the thermal diffusivity. For air, Pr is approximately 0.7, depending slightly on
temperature.3 The product, Gr*Pr is the Rayleigh number, Ra, which can be used to
find the Nusselt number. The relationship between Nu and Ra is empirical. For this,
we must turn to a heat transfer text.4 As we will
see, Ra is about 1010,
which puts us at the top of the transition region and into the
turbulent region, where
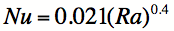 (3)
This applies to vertical plates or cylinders alike, either of
which is a reasonable approximation to the human body.
(3)
This applies to vertical plates or cylinders alike, either of
which is a reasonable approximation to the human body.
Finally, it is time to plug in some numbers. Human skin temperature5 is about 34°C. However, if the person is clothed, the effective surface temperature will be lower, say 30°C. For 20°C ambient temperature, ΔT=10°C=10K. For an adult, L=2 m. Then Ra=8x109, resulting in Nu of about 200. This large value justifies neglecting conduction since Nu is the ratio of convective to conductive thermal transfer rates. Since k=0.026 W/m/K for air,3 the convective thermal flux rate is
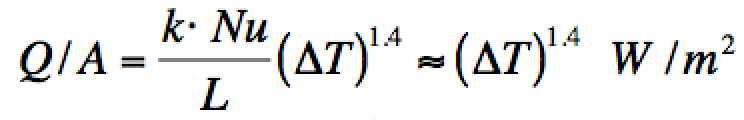 (4)
(4)
3. Radiation
For comparison, the radiation rate is determined by the Stefan-Boltzmann Law,
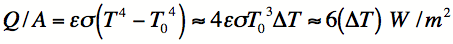 (5)
where T0 is
the ambient absolute temperature, ε is the emissivity, and σ is
the Stefan-Boltzmann constant. For skin or clothing, emissivity
is near unity. This approximation is valid when ΔT is small compared to the
ambient temperature, T0.
(5)
where T0 is
the ambient absolute temperature, ε is the emissivity, and σ is
the Stefan-Boltzmann constant. For skin or clothing, emissivity
is near unity. This approximation is valid when ΔT is small compared to the
ambient temperature, T0.
4. Comparison of convective and radiative rates
The ratio of convective to radiative transfer is only weakly dependent on temperature difference:
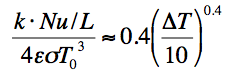 (6)
Hence, the assumed value for ΔT
of 10°C is not critical to the comparison of the relative
importance of convection and radiation. The convective heat loss
rate is about half the radiative rate. Forced convection will
increase this ratio (cf.
Sec. 5).
(6)
Hence, the assumed value for ΔT
of 10°C is not critical to the comparison of the relative
importance of convection and radiation. The convective heat loss
rate is about half the radiative rate. Forced convection will
increase this ratio (cf.
Sec. 5).
5. Other work
This topic has been discussed by others. For example, Flores6 estimates the free convection coefficient of 2.3, compared to 2.6 in Eq. (4) above. Assuming a wind of 1 mph (~0.5 m/s), Flores estimates a 40% enhancement of the convective rate.
Lee7 modeled a clothed human. His model predicts that the ratio of convective to radiative heat loss is 0.7 at an ambient temperature of 20°C, somewhat higher than predicted by Eq. (6). This result was independent of the air gap between skin and fabric. The model was validated by an experimental simulation of a clothed human body by a hot plate covered with fabric. Lee's model did assume a slight wind, 0.2 m/s, though the experimental setup did not.
Hardy and DuBois8 reported basal metabolic rates of two subjects (themselves), finding a rate of about 35 kcal/m2/hr or 41 W/m2. This is not consistent with the values computed using Eqs. (4) and (5) for ΔT>5K. This can be explained by the fact that the (nude) subjects were not in a steady state; they were losing energy more rapidly their metabolism was able to replace it. As the authors note, "...both subjects were on the point of shivering at the end of the basal periods in many experiments in which the temperature was lower than 27°C." They subsequently began to shiver. Curiously, these authors reported very low convection rates (10 - 20% of the total), with the highest rates at the smallest temperature differences. This contradicts the prediction of Eq. (6). They did not explain how convective rates were measured.
DeDear, et al.,9 measured radiative and convective thermal loss rates rates using manikins. They found the convective rate to be 3.3 W/m2/K, somewhat higher than Eq. (4) predicts. This is not surprising given the uncertainties in the calculation. They also measured 4.5 W/m2/K for the radiative rate, rather lower than predicted by Eq. (5). This discrepancy is likely caused by a lower emissivity than assumed in Sec. 3. The value obtained by deDear, et al. is consistent with emissivity 0.8. In the presence of 1m/s wind these authors found an additional 10 W/m2/K of forced convective loss.
6. Conclusions
Even in the absence of wind, convection is an important mechanism in cooling the human body. Under such conditions, convection accounts for about 1/3 the thermal loss of the human body in cool, still air. As other thermal loss mechanisms grow in importance, such as forced convection and perspiration, radiation assumes a minor role in human thermal balance. This is consonant with the concept of "wind-chill" factor, which accounts for the enhanced sensation of cold when it is windy. These conclusions are only weakly dependent on the assumed temperature of clothing or skin, which is only estimated rather crudely.
7. Acknowledgments
I am grateful for the assistance of Edward Ruf, who provided a crucial reference and insight into the physics of convection. I am also indebted to Fred Kinley who also provided useful references.
8. References
1. Eric Weisstein, World of Physics, http://scienceworld.wolfram.com/physics/NusseltNumber.html
2. Eric Weisstein, World of Physics, http://scienceworld.wolfram.com/physics/GrashofNumber.html
3. The Engineering Toolbox, http://www.engineeringtoolbox.com/air-properties-d_156.html
4. Frank Kreith and William Z. Black, Basic Heat Transfer (Harper & Row, Publishers, Inc. NewYork, NY 1980).
5. Hypertextbook, http://hypertextbook.com/facts/2001/AbantyFarzana.shtml
Temperature Regulation in the Neutral Zone, http://faculty.washington.edu/brengelm/neut_zone/pg1.html
Cooling of the Human Body, http://hyperphysics.phy-astr.gsu.edu/Hbase/thermo/coobod.html
6. Juan G. Flores in Biomedical Engineering Principles, D.O. Cooney, ed., (Marcel Dekker, New York, NY, 1976). https://www.scribd.com/document/44607050/Heat-Transefer-Coefficient-of-Human
7. Bin Lee, Theoretical Prediction and Measurement of the Fabric Surface Apparent Temperature in a Simulated Man/Fabric/Environment System (DSTO Aeronautical and Maritime Research Laboratory, 1999)
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.484.2110&rep=rep1&type=pdf
8. J.D. Hardy and E.F. DuBois, Proc. Nat Acad. Sci., 23, 624 (1937).
http://www.pnas.org/cgi/reprint/23/12/624.pdf
9. de Dear, R. J.; Arens, Edward; Hui, Zhang; Oguro, Masayuki, International Journal of Biometeorology, 40, 141 (1997).
http://adsabs.harvard.edu/abs/1997IJBm...40..141D
Humans, and animals in general, are usually in a thermal steady state with respect to their surroundings. In particular, endotherms seek to control their body temperatures. Heat generated by metabolic processes is lost to the environment though several mechanisms: radiation, conduction, convection, and evaporation. Unless the organism has more heat than can be eliminated by radiation and convection, evaporation (through perspiration) is not required and conduction is negligible (cf. section 2). This is most relevant when ambient temperatures are low (e.g., winter). While radiation is easily estimated, convection requires more effort and some assumptions.
2. Free convection
Convection relies on the flow of a fluid to transport heat from the object being cooled to the surrounding environment. In free convection, this fluid motion is the result of the buoyancy of warmer fluid in the cooler surrounding fluid. If there is an externally imposed flow, such as a wind, the convective rate is enhanced. At the very least, heat will be removed at the rate due to free convection. The Nusselt number is the ratio of the hard-to-compute convective transfer rate to the easy-to-determine conductive rate:1
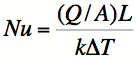 (1)
(1)
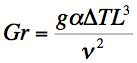 (2)
(2) 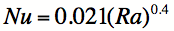 (3)
(3) Finally, it is time to plug in some numbers. Human skin temperature5 is about 34°C. However, if the person is clothed, the effective surface temperature will be lower, say 30°C. For 20°C ambient temperature, ΔT=10°C=10K. For an adult, L=2 m. Then Ra=8x109, resulting in Nu of about 200. This large value justifies neglecting conduction since Nu is the ratio of convective to conductive thermal transfer rates. Since k=0.026 W/m/K for air,3 the convective thermal flux rate is
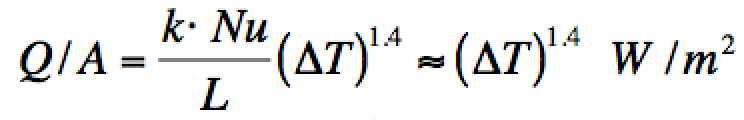 (4)
(4) 3. Radiation
For comparison, the radiation rate is determined by the Stefan-Boltzmann Law,
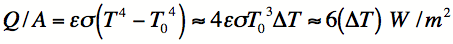 (5)
(5) 4. Comparison of convective and radiative rates
The ratio of convective to radiative transfer is only weakly dependent on temperature difference:
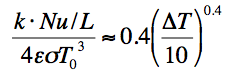 (6)
(6) 5. Other work
This topic has been discussed by others. For example, Flores6 estimates the free convection coefficient of 2.3, compared to 2.6 in Eq. (4) above. Assuming a wind of 1 mph (~0.5 m/s), Flores estimates a 40% enhancement of the convective rate.
Lee7 modeled a clothed human. His model predicts that the ratio of convective to radiative heat loss is 0.7 at an ambient temperature of 20°C, somewhat higher than predicted by Eq. (6). This result was independent of the air gap between skin and fabric. The model was validated by an experimental simulation of a clothed human body by a hot plate covered with fabric. Lee's model did assume a slight wind, 0.2 m/s, though the experimental setup did not.
Hardy and DuBois8 reported basal metabolic rates of two subjects (themselves), finding a rate of about 35 kcal/m2/hr or 41 W/m2. This is not consistent with the values computed using Eqs. (4) and (5) for ΔT>5K. This can be explained by the fact that the (nude) subjects were not in a steady state; they were losing energy more rapidly their metabolism was able to replace it. As the authors note, "...both subjects were on the point of shivering at the end of the basal periods in many experiments in which the temperature was lower than 27°C." They subsequently began to shiver. Curiously, these authors reported very low convection rates (10 - 20% of the total), with the highest rates at the smallest temperature differences. This contradicts the prediction of Eq. (6). They did not explain how convective rates were measured.
DeDear, et al.,9 measured radiative and convective thermal loss rates rates using manikins. They found the convective rate to be 3.3 W/m2/K, somewhat higher than Eq. (4) predicts. This is not surprising given the uncertainties in the calculation. They also measured 4.5 W/m2/K for the radiative rate, rather lower than predicted by Eq. (5). This discrepancy is likely caused by a lower emissivity than assumed in Sec. 3. The value obtained by deDear, et al. is consistent with emissivity 0.8. In the presence of 1m/s wind these authors found an additional 10 W/m2/K of forced convective loss.
6. Conclusions
Even in the absence of wind, convection is an important mechanism in cooling the human body. Under such conditions, convection accounts for about 1/3 the thermal loss of the human body in cool, still air. As other thermal loss mechanisms grow in importance, such as forced convection and perspiration, radiation assumes a minor role in human thermal balance. This is consonant with the concept of "wind-chill" factor, which accounts for the enhanced sensation of cold when it is windy. These conclusions are only weakly dependent on the assumed temperature of clothing or skin, which is only estimated rather crudely.
7. Acknowledgments
I am grateful for the assistance of Edward Ruf, who provided a crucial reference and insight into the physics of convection. I am also indebted to Fred Kinley who also provided useful references.
8. References
1. Eric Weisstein, World of Physics, http://scienceworld.wolfram.com/physics/NusseltNumber.html
2. Eric Weisstein, World of Physics, http://scienceworld.wolfram.com/physics/GrashofNumber.html
3. The Engineering Toolbox, http://www.engineeringtoolbox.com/air-properties-d_156.html
4. Frank Kreith and William Z. Black, Basic Heat Transfer (Harper & Row, Publishers, Inc. NewYork, NY 1980).
5. Hypertextbook, http://hypertextbook.com/facts/2001/AbantyFarzana.shtml
Temperature Regulation in the Neutral Zone, http://faculty.washington.edu/brengelm/neut_zone/pg1.html
Cooling of the Human Body, http://hyperphysics.phy-astr.gsu.edu/Hbase/thermo/coobod.html
6. Juan G. Flores in Biomedical Engineering Principles, D.O. Cooney, ed., (Marcel Dekker, New York, NY, 1976). https://www.scribd.com/document/44607050/Heat-Transefer-Coefficient-of-Human
7. Bin Lee, Theoretical Prediction and Measurement of the Fabric Surface Apparent Temperature in a Simulated Man/Fabric/Environment System (DSTO Aeronautical and Maritime Research Laboratory, 1999)
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.484.2110&rep=rep1&type=pdf
8. J.D. Hardy and E.F. DuBois, Proc. Nat Acad. Sci., 23, 624 (1937).
http://www.pnas.org/cgi/reprint/23/12/624.pdf
9. de Dear, R. J.; Arens, Edward; Hui, Zhang; Oguro, Masayuki, International Journal of Biometeorology, 40, 141 (1997).
http://adsabs.harvard.edu/abs/1997IJBm...40..141D