The Sounds of Teacups and Glasses

The Sounds of
Teacups and Glasses

1.0 Introduction

The sound of a tapped glass or cup depends on the height of the fluid. The pitch may also depend on other factors. For example, when powdered cocoa is dissolved in water, some observers report changes in pitch.¹ Sometimes, just the act of stirring is purported to cause a pitch change. There are even some explanations of this phenomenon.² The purpose of this page is to summarize the current state of knowledge on this complicated question.

Is this trivial? Sure it is. Silly? Maybe. There is a lot of good physics in such seemingly trivial problems. Remember Feynman's sprinkler problem?³

2.0 How pitch changes with fluid level

One might expect the pitch to rise with fluid level since the height of the air column and the length of glass above the waterline decreases as the fluid level rises. Indeed, this is the explanation offered at Tuneful Tea:
"In the case of a cup of tea, the freeboard (the distance from the surface of the tea to the rim of the cup) is important. An empty cup has a low ping and a full cup has a high ping. Technically, the length of the resonant element (the side of the cup) is shortened when the cup is full, hence a higher frequency."

Too bad it doesn't agree with experiment. Obviously, the author of these words never tried it! As any glass harmonica player can tell you, pitch falls with higher water level. Here are the spectra for an empty brandy glass and a full one:

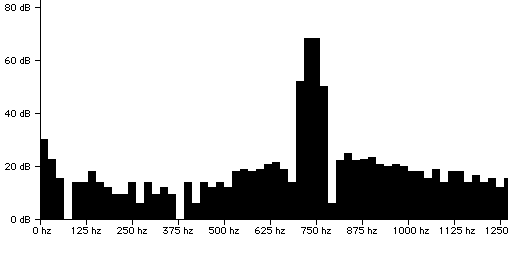
Fig. 2.1. Empty glass (Listen to the sound by clicking on the link.)

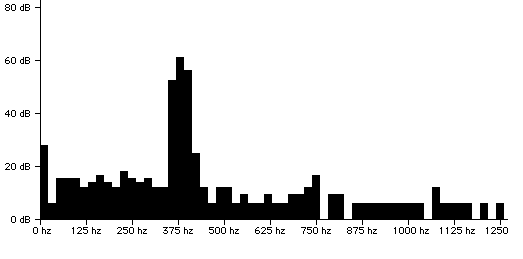
Fig. 2.2. Full glass (Listen to the sound by clicking on the link.)

There is a continuous progression of lower frequencies as the glass is filled. The pitch drops about an octave. Similar spectra are obtained for ceramic mugs, although they are much more heavily damped:
empty cup
full cup

So, the pitch drops... but why? My hypothesis is that the water is moved by the vibration and that the restoring force is provided by the vessel. The restoring force is approximately independent of water level. I assume that water is incompressible. This is reasonable since it is much easier to deform the glass than to compress the fluid.

Since the resonant frequency is proportional to the square root of the force constant divided by the mass, more fluid implies a lower frequency. As the fluid level rises, the pitch drops because there is more mass to move. The speed of sound in the water is irrelevant.

3.0 How pitch changes with dissolved material

Theory

Tuneful Tea also describes the changes in the sound of a cup as powders are dissolved. The hypothesis is advanced that air bubbles that accompany the powder change the speed of sound in the fluid. See also Jearl Walker's entertaining book.⁴ This contradicts the idea that the fluid is incompressible. These two views can be reconciled by realizing that a small contamination of water by air bubbles dramatically changes the compressibility.

The speed of sound in a medium is given by:

In an ideal gas, the speed of sound is given by the familiar expressions:

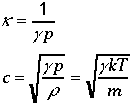
Let be the fraction (by volume) of air dissolved in water. The density and compressibility of the composite medium are

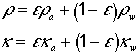
where the a and w subscripts refer to air and water, respectively.
The speed of sound in the composite medium is

The approximation was made that pure water is incompressible. Also, the density of air was neglected compared to that of water. This means that the equation is not valid for very near zero or unity. The regime of interest is covered by the approximations.

Assume that the volume fraction of air bubbles is 1%. The speed of sound in the medium is about 120 m/s, lower than it is in air! This is reasonable since the mean density of water has hardly changed, but the compressibility is much greater. One can imagine higher volumetric concentrations of air, resulting in even lower sound speeds. The graph below shows the relationship between the speed of sound and the volume fraction of water. The approximate formula is accurate to within a few percent for volume fractions between 10^-3 and 0.98.

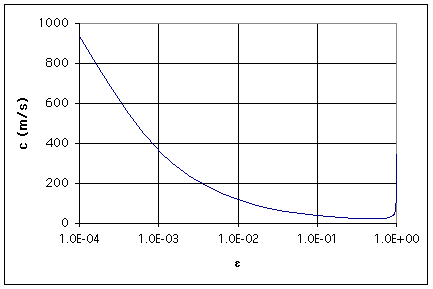
Unlike the case of pure water, the lower sound speed and higher compressibility means that the fluid is participating in the oscillation with compression and rarefaction. The fluid's sound speed governs the resonant frequency.

Experiment

Air was introduced in water using an ordinary aerator in a water tap. A 8-cm inner diameter, 8-cm deep mug was filled to a depth of 7.5 cm. Approximately 0.25 sec after filling the cup, the bottom was tapped once with a metal spoon. After another 3.5 sec, the bottom was tapped again. Here are the spectra for these two cases:

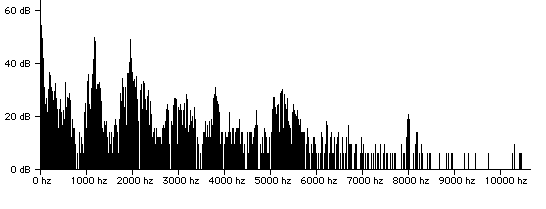
Fig. 3.1. Aerated-water spectrum at t = 0.25 sec with 22 Hz resolution.
(Listen to the sound by clicking on the link.)

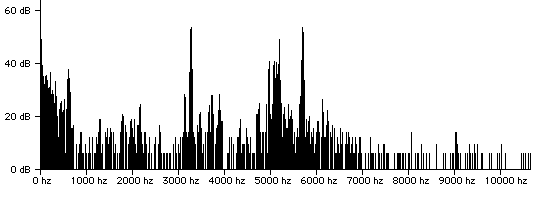
Fig. 3.2. Water spectrum at t = 3.75 sec with 22 Hz resolution.
(Listen to the sound by clicking on the link.)

The aerated-water spectrum has a resonance at 1200 Hz. This probably corresponds to a quarter-wave open pipe resonance with a wavelength of 0.3 m. This implies an effective sound velocity of c=(1200)(0.3)=360m/s. The expression above for c in terms of the volumetric air fraction results in

The line near 2000 Hz is likely a higher-order mode, possibly including transverse excitation.

After the bubbles have dissipated, the lowest resonance is at about 3300 Hz, almost three times higher than in aerated water. The quarter-wave resonance with c=1500m/s (pure water sound speed) would be at about 5000 Hz. The features at 5200 and 5700 Hz are candidates.

When the full cup (filled to 7.5 cm depth) was tapped on the side, the spectrum was quite different:

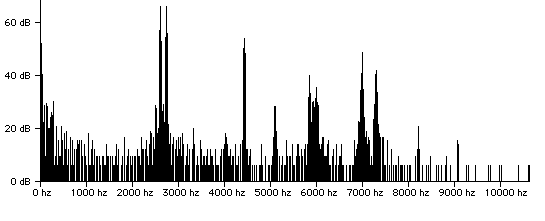
Fig. 3.3. Water spectrum of full cup tapped on the side (22 Hz resolution).
(Listen to the sound by clicking on the link.)

New features appear that probably correspond to the flexure resonances of the cup itself. Most lines are heavily damped, with the exception of the doublet at about 2500 Hz and the line at 4400 Hz. The spectra of a full cup tapped on the bottom and the side (Figs. 3.2 and 3.3, respectively) have virtually no features in common. This supports the interpretation of the spectral lines as in Fig. 3.2 as being due to resonances of the water column. More bottom vs side sounds here: Side vs. Bottom.

Acknowledgements

The author is grateful to W.L. Shackleford and J.W. Dooley for their comments and insights.

References
¹W.L. Shackleford, personal communication.
See also, Science Q&A .
²See Tuneful Tea .
³Richard Feynman, "Surely You're Joking Mr. Feynman!": Adventures of a Curious Character (W.W. Norton & Co., 1997). See also the Edgerton Center page on this at MIT.
⁴Jearl Walker, The Flying Circus of Physics With Answers, p. 6 (John Wiley & Sons, 1977).

If you have any thoughts or experimental results, I would like to hear about them. Write me at

Home | Syllabus | Readings | Math | Physics Links